Technical information on the molecular planetary gear

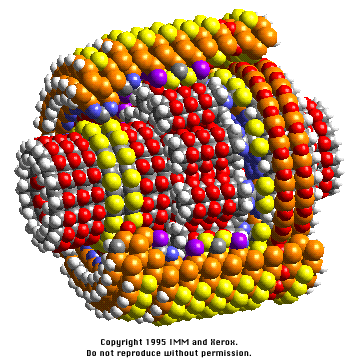
This page provides more technical information about the planetary gear than the non-technical introductory page.

The current version of the planetary gear is available in three formats:

Molecular Dynamics

Several people have expressed interest in performing molecular dynamics calculations on the planetary gear. As several important properties of the planetary gear are currently not well understood (including the maximum speed of operation that is feasible, the maximum torque that can be applied, etc) the "best" modeling conditions are not currently known.

At the most basic level, the maximum 0 kelvin static torque is not known, and is likely to vary at least somewhat with the particular potential energy function used. To determine the maximum static torque, it is necessary to:

  1. Prevent rotation of the planet carrier.
  2. Prevent rotation of the casing.
  3. Apply a known torque to the sun gear.
  4. Optimize the geometry by minimizing the energy.
  5. Determine whether the planetary gear failed (by visual inspection).
  6. Increase or decrease the torque as appropriate, and go to step 3.
There are several ways of doing items 1 and 2, the simplest being to select some subset of the atoms in the planet carrier and casing and freezing their locations. The chosen atoms should preferably be as remote from the active part of the planetary gear as feasible. Several other methods could be used.

Item 3 can be done in one of two ways: actually apply a torque to the sun gear and minimize, presumably by applying the desired force to a subset of the atoms of the sun gear (again, as far removed from the active region of the planetary gear as feasible); or alternatively by selecting a subset of the atoms in the sun gear, rotating them by some small amount, freezing their locations, and minimizing. After minimization, the forces on the frozen atoms would permit computation of the applied torque.

Note that the maximum 0 kelvin static torque that can be tolerated by the planetary gear will differ from the static torque that could be tolerated at some higher temperature (such as 300 kelvins), as thermal noise implies that there will be some finite probability that the planetary gear will fail (slip a gear, break off a planet, or whatever) when the applied torque is significantly lower than the maximum 0 kelvin static torque. Presumably, if the applied static torque is sufficiently reduced, the probability of failure at higher temperatures can be made very small -- unless, of course, the barrier against failure is of the same order of magnitude as kT. This is hopefully unlikely with the current structure at "reasonable" operating temperatures.

Once knowing the maximum 0 kelvin static torque that can be applied, the planetary gear could be accelerated from rest to higher and higher rotational speeds by:

  1. Preventing rotation of the casing.
  2. Applying a torque that is a modest fraction of the maximum 0 kelvin static torque (perhaps 5%).
  3. Watching the planetary gear accelerate to higher and higher rotational speeds, until
  4. At some sufficiently high speed, the planetary gear fails (note that the use of a Morse potential for bonds would likely result in a particularly spectacular failure mode....)
Another method of determining whether or not the planetary gear will function at a given frequency would be to start all components of the structure moving with approximately the correct velocities, and then observe the resulting behavior. This, of course, requires that we be able to generate some approximation to the correct initial velocities for each atom. This might be done in the following manner:
  1. Starting with the minimized structure, rotate each planet clockwise by 0.1 "teeth".
  2. Rotate the casing clockwise by 0.1 "teeth".
  3. Rotate the sun gear counterclockwise by 0.1 "teeth".
  4. Minimize the new structure.
  5. Align the casing of the new structure with the casing of the old structure.
  6. For each atom, compute the difference between its old position and its new position.
  7. Treat the resulting vectors as an approximation to the direction of motion of each atom during normal movement of the planetary gear.
  8. Scale the velocity vectors to correspond with the desired frequency of operation (and perhaps add "thermal noise" to the velocity vectors, corresponding to the desired temperature of operation, e.g., 300 kelvins).
  9. Prevent rotation of the casing.
  10. Apply the proper fixed rotational speed to a subset of atoms selected from the sun gear.
  11. Use molecular dynamics to watch the behavior of the resulting system. Again, use of the Morse potential for bonds should result in a spectacular display when the planetary gear is operated at a sufficiently high frequency.
The rotation by "teeth" is a convenient measure, but for each component the actual angular rotation to apply will be different. Molecular dynamics both of normal operation and of failure modes should be interesting, and the resulting videos are likely to show quite graphically what types of failure occur first. The failure modes will presumably suggest design changes which would permit higher speed (or higher torque) operation; or otherwise suggest design improvements.

A simulation of the original planetary gear in which the sungear was given an instantaneous initial rotational speed of 500 gigahertz was done at Caltech. Under these conditions, the original design did not work satisfactorily, exhibiting frequent slippages. It is quite plausible that the current design would fail under such conditions as well.